相比之下这篇论文的可读性感觉比较高,至少我这个英语白痴初见也能基本看懂在说什么……
但是里面 2,3 节出现的一些公式还是有些啃不懂,根据上下文的解释囫囵的理解了一下……对于一些新出现的名词也是根据课外以及查询 ai 理解了一下。
前情提要:
Proximal Policy Optimization (PPO)
近端策略优化
核心思想在于,为了防止因为模型改变习惯太猛而导致训练崩溃,引入 clip ,大意为每次训练的最大修改的区间,来保持训练的稳定性。
Group Relative Policy Optimization(GRPO)
这是 DeepSeek 提出的一种改进版算法。
与PPO最大最关键的区别是,PPO 要训练两个模型,一个负责做题,一个负责打分,而后者模型通常和前者一样大,非常占显存,费算力。
所以 GRPO 直接省略了打分模型,而是针对同一个问题,一口气生成 G 个 不同的答案。 打分不看绝对分数,而是看相对排名。
Removing KL Divergence
KL 散度是什么:在传统的聊天机器人训练(RLHF)中,我们希望模型“说话像人”。为了防止模型为了拿高分而开始胡言乱语(比如一直重复一个词),我们会加一个KL 惩罚项。作用在于: 它不让它离“原始模型(Reference Model)”太远。如果偏离太远,就扣分。
但我们现在要 训练数学推理模型。模型一开始不会做题,如果用 KL 散度把它拴在原始模型身边,效果很差。
所以移除 KL 散度。
Rule-based Reward Modeling
Reward Hacking:在写诗或聊天任务中,好坏很难评判,通常需要训练一个奖励模型来打分。但这很容易出问题,模型可能会学会去讨好这个打分 AI ,而不是真的写的好。
哎!但是话又说回来,我们在训练数学推理模型,所以结果是唯一的,所以不搞那么多虚头巴脑的,直接根据答案是否正确给分,对了加一分,错了减一分。
核心内容
Clip-Higher
在 PPO 类算法中,为了防止策略更新过大导致训练不稳定,会使用 clip 函数将新旧策略的比率 $$ r_t(\theta) = \frac{\pi_\theta}{\pi_{old}} $$
限制在 $$ [1-\epsilon, 1+\epsilon] $$ 之间。 作者观察到“熵坍缩(Entropy Collapse)”现象:模型很快变得过于自信,只输出固定的某种答案,停止了探索。
传统的对称裁剪存在非对称的影响:
- 高概率词元(Exploitation): 假设旧概率是 0.9。上限是 0.9 × (1+0.2) = 1.08 。因为概率不可能超过 1,所以这个上限实际上不起作用。模型可以轻易地将概率从 0.9 推到 0.999。
- 低概率词元(Exploration): 假设旧概率是 0.01(这是模型尝试探索的新路径)。上限是 0.01 × 1.2 = 0.012。模型想探索这个新路径,但被死死限制在 0.012,几乎无法增长。为了解决这个问题,有了下面的方法。
将上下界解耦,设置两个不同的参数 $\epsilon_{low}$ 和 $\epsilon_{high}$
- 保持前者不变(防止概率降为 0 导致采样空间坍缩)。
- 显著调高后者(例如从 0.2 调到 0.28 或更高)。
允许低概率的“探索性”词元在单次更新中获得更大的增长幅度,从而维持策略分布的多样性,防止模型过早陷入局部最优。
btw,我猜测后续要做的代码微调中,$\epsilon_{high}$就是重要的一环。
Dynamic Sampling(动态采样)
GRPO 算法依赖于“组内优势”计算,公式为 $ A_i = \frac{R_i – \text{mean}(R)}{\text{std}(R)} $。 随着训练进行,模型能力变强,会出现两种导致梯度消失的极端情况:
- 全对: 一组采样的 G 个答案全部正确(Reward 全为 1)。此时 Mean=1, Std=0。
- 全错: 一组采样全部错误。此时 Mean=-1, Std=0。
在这些情况下,优势无法计算或为零,导致该批次数据的有效梯度为零。随着模型变强,“全对”的样本越来越多,实际参与更新的有效样本数(Effective Batch Size)急剧下降,导致训练效率降低,梯度方差变大。
解决方案: 引入动态采样机制,核心逻辑包含两步:
- 过滤: 在计算梯度前,直接剔除掉那些“全对”或“全错”的 Prompt),因为它们提供不了相对优势信息。
- 过采样(Over-sampling): 在数据采集阶段,持续采样,直到填满一个 Batch 的有效样本(即组内既有对也有错的样本)。
这样,保证了在整个训练周期内,每一个 Batch 都能提供充足、有效的梯度信号,很好理解,解决了训练后期收敛变慢的问题。
Token-Level Policy Gradient Loss
原始 GRPO 计算损失时采用的是 Sample-Level 平均。 即:先计算一个回答中所有 Token 的平均损失,得到该样本的 Loss,再与其他样本的 Loss 求平均。$ L_{total} = \frac{1}{G} \sum_{i=1}^{G} (\frac{1}{Length_i} \sum_{t=1}^{Length_i} L_{token})$
这种平均化操作导致长样本(Long CoT)和短样本在梯度贡献上是等价的。
- 在长思维链推理中,每一个推理步骤都很重要,样本级平均稀释了长序列中关键步骤的信号。
- 如果模型生成了超长的乱码(Gibberish),样本级平均无法根据“乱码数量”给予足够强烈的惩罚。
解决方案: 改为 Token-Level(词元级) 求和。 不再在样本内部求平均,而是将一个 Batch 内所有样本的所有 Token 的损失直接加总(或者加权使得长样本权重更大)。$ L_{total} = \frac{1}{\sum Length} \sum_{i=1}^{G} \sum_{t=1}^{Length_i} L_{token} $
作用:
- 权重重分配: 长序列(包含更多推理步骤)对梯度的贡献更大,符合 Long-CoT 的特性。
- 抑制乱码: 如果模型生成长篇乱码,Token 级损失会累积产生巨大的惩罚信号,从而更有效地抑制这种行为,控制生成长度的恶性膨胀。
Overlong Reward Shaping(超长奖励重塑)
模型推理受限于最大上下文长度。如果生成超长被强制截断(Truncation),通常会被视为“错误”,给予 -1 的奖励。 这引入了奖励噪声(Reward Noise):模型可能推理是对的,只是写得太长被截断了,这会混淆模型。
解决方案作者提了两个:
- Overlong Filtering(截断过滤): 最简单的办法,直接丢弃被截断的样本,不让它们参与梯度计算,避免错误信号干扰。
- Soft Overlong Punishment(软性超长惩罚): 设计一个基于长度的惩罚函数 $ R_{length} $。
- 安全区: 长度未接近上限时,不惩罚。
- 缓冲特定区(Cache): 在接近上限的一段区间内,随着长度增加,线性施加负奖励。
- 截断区: 超过上限,给予 -1。
Dataset Transformation
数学题的答案格式千奇百怪。使用正则表达式(Regex)去解析模型的输出并与标准答案匹配,极易出错。 解析错误 = 错误的奖励信号 = 训练失败。
解决方案: 利用 LLM 改写题目,将所有问题的答案强制转换为整数(Integer)形式。
Decoupled Clip and Dynamic Sampling Policy Optimization(DAPO)
DAPO具体就是在GRPO的基础上经过以上5小节的优化(Clip-Higher + 动态采样 + Token级损失 + 软惩罚)提出的新架构。
值得学习的写论文技巧:
如下表:
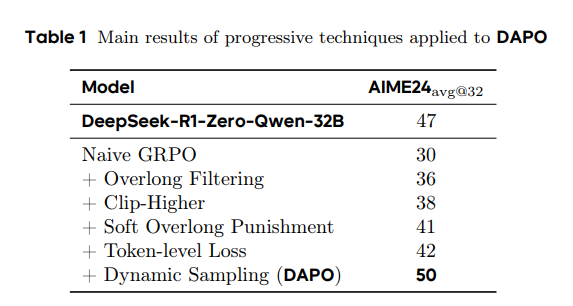
展现数据可以一层层展现,这样可以有力说明我算法的每一步都是有效的。
另外作者在 4.3 节教了 RL 训练真正该看什么:
- 看熵(Entropy):
- 太低 = 模型不思考了(坍缩)。
- 太高 = 模型在胡言乱语(乱码)。
- 要保持“缓慢上升”的趋势。
2. 看长度(Length):
RL 的神奇之处在于,没人教模型写长,它为了做对题,自己学会了写长步骤。如果长度突然不涨了,或者开始变短,说明训练可能出问题了。
3. 看奖励(Reward):
作者指出了一个残酷的真相:训练集上的奖励涨了,不代表验证集能得分(过拟合)。
启示: 做实验时,一定要记录这些中间指标。当实验失败时,这些曲线也许能指出到底死在哪一步。
作者用的训练参数(开抄(x))
基础模型: Qwen2.5-32B
优化器: AdamW
学习率: 1e-6 (恒定/Constant)
预热步数: 20 个 Rollout steps (线性预热)
KL散度系数: 0 (明确移除KL惩罚)
下界裁剪 ($epsilon_low$): 0.2
上界裁剪 ($epsilon_high$): 0.28 (关键参数)
采样组大小 (G): 16 (每个Prompt生成16个回复)
最大生成长度 (Hard Max): 20480 tokens
软惩罚起始长度: 16384 tokens
软惩罚缓冲区的长度: 4096 tokens
(逻辑: 长度超过16384后开始线性扣分,超过20480直接判负)
采样提示词批次 (Rollout Batch): 512
训练小批次 (Mini-batch): 512
每轮梯度更新次数: 16次
Temperature: 1.0
Top-p: 0.7
评估采样次数: 32次 (取平均值 avg@32)
0 条评论